TRUTH EXISTS. LOGIC IS EXISTENCE

What is the most important discovery science ever made?

That truth exists.

Science, logic, emotion, even truth, are all local. Whereas the universe, as far as we can see, extends without bounds shrouded in more mystery than we can guess. Truth is local, but shines and makes us, locally, divine. Most of what there is has to be revealed yet [1]. 

But for the most important: truth exists.

***

SCIENCE POINTS OUT EXISTENCE And CREATES IT:

Demonstrate, comes from what comes out (“de“) of showing (“monstrare“). Trying to temper my seemingly fanatical pro-science mood, as if one needed to be tempered in one’s thirst for knowledge, Sagal Tisqaad made an age-old objection:

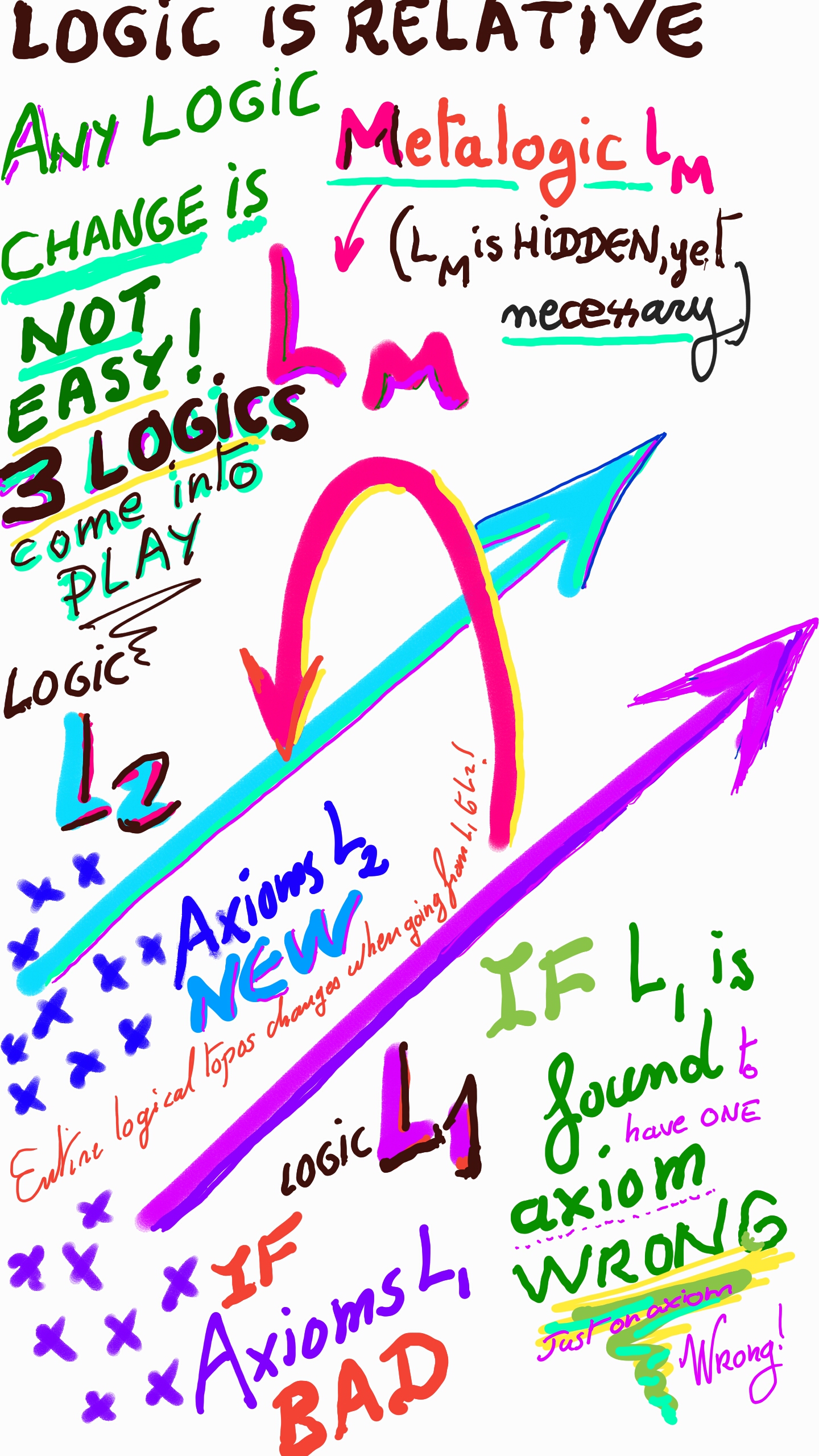
“Science has only ever explained how things work. Not what they are.”

Right. Except that things are defined by how they look and how they work… Exactly as “science” does it. And “science” means (more or less) certain knowledge. No more no less. Being against it is being against brains. But then there is more… Is an explanation itself an… object? Yes it is!Let me explain after the contemplation of the tree of life…

Actually some of the basic Judeo-Christian texts evoke the “logic of life”.

LOGOS IS EXISTENCE, EXISTENCE IS LOGOS:

Explaining how something works, and what it means, to work, is itself an existentialist statement. If I proffer Proposition P,  there exists P. 

Some may whine that is just sophistry, a mind game. However, minds are real objects.

At least, so I claim.  I view the brain as a dynamic (sub) quantic object [2]… Made of patterns (neurons, axons, dendrites, neurohormonal topology, and the geometry and topology of structures we know nothing about yet, because they are too fine and dynamic for our present gross instruments of scientific inquiry to reveal; an example is the inner machinery of just one neuron, which is most certainly, in part, and among other things, a Quantum Computer, a sort of entity we barely know exist, and how to make it work a tiny bit… even with the the help of tremendous machinery…)

Ideas correspond to neural geometry-topological patterns, so to a proposition P is associated such a pattern, a pattern specific to P… which didn’t exist before, so came into being as the idea got formulated (one will generally utter the idea before really formulating it). 

“In other words, logic creates existence. As John had it in the Bible…

“In the beginning was the Logos, and the Logos was with God, and the Logos was God.” (John 1;1)

Ἐν ἀρχῇ ἦν ὁ λόγος, καὶ ὁ λόγος ἦν πρὸς τὸν θεόν, καὶ θεὸς ἦν ὁ λόγος (En arkhêi ên ho lógos, kaì ho lógos ên pròs tòn theón, kaì theòs ên ho lógos.) The concept is already in Luke 1;2 and the Book of Revelation [3]…

Identifying God and Logic was explicitly done in the 11C by a prominent abbot to the fury of the Catholic church and its Pope. That was the beginning of the end of Christianism. 

How did antique thinkers realize that the logos (discourse, logic) entails existence? Well, introspection: when one has an idea or song in one’s head it can feel all too real… And could, in the end, move mountains… So exist it does…

Patrice Ayme

***

P/S: If I put my hand on a red hot surface, what comes into being? Pain! Is pain a… logos… according to my conceptology above? Of course. Pain is logos, fresh or not. Pain is a pattern in the brain which comes into existence, with plenty of sense attached to it, and pain has to co-exist with the rest of pre-existing patterns in said brain…

***

[1] How can something exist locally and not globally? Casual observations show this is the case. Differential geometry is all about the interplay between local and global. That means there is a gigantic science of the interplay between local and global, which can be used… both globally and locally in various analogies, more or less valid or evocative…

*** 

[2] This does not depend on the first analysis, upon my SQPR, underlying CIQ (Copenhagen Interpretation of Quantum). It could well be that ideas could be viewed as classical objects. 

***

[3] λόγος, logos is often mistranslated as “word” by churchmen, who, understandably enough, fear logic, the logos. In truth logos is not just the “word”, but words with sense attached, as in Category Theory… logos, the discourse, the logic. Oh, what is logic? No logician has a wide enough concept of “logic”. It is an open problem in logic, what logic is. What I propose is that logic is any brain arrangement which makes sense (by making sense, I mean a sense like x–>y… any chain of implications, as in Category Theory…) 

 

Pure Logic Is An Illusion. Axiomatics Means Choice, Thus Heresy.

The problem with pretending that there is something as pure logic is that any logical system involves axiomatic choices, and those, in turn, are a matter of emotions, feelings, proclivities, inclinations, and, generally sentiment, thus emotion. 

This initial axiomatic choice is even more basic than Second Order Logic Incompleteness theorems (which say that, given an axiomatic and basic arithmetic, one will still have to make further emotional choices down the logical road, beyond the initial axiomatic system).

It is not easy to find good and complete axiomatics. Euclid had five axioms, but he took for granted other axioms or operations which he used, but did not mention as the axioms they were. For example that a line divided the plane. With his fifth axiom, the parallel axiom, Euclid disappeared non-Euclidean geometry, which existed before and allowed to compute the size of the Earth, distance of Moon and Sun, etc. so Euclid, in one sense, shrunk minds.

In other words, a logical system will be as smart as what we want to do with it… An emotional will, so to speak. Emotional wills can be pretty stupid, as when religious fanatics want to kill everybody. The most famous case in history happened during the Crusade against the Albigeois in France when the legate of the Pope was asked how to distinguish good Catholics from heretics, and he replied: “Kill them all, God will recognize his own!”

In the European Middle Ages, the basic emotion in the matter of civilization among most people is that they owed the world to “God”. Later that emotion was overwhelmed by the realization that attributing fascism to a Dog in the sky, had been a collective illusion to make possible the rule of the few. The USA is presently undergoing such a transformation, as the belief in “God” is collapsing… in no small part due to its subconscious connection to the established order… which is entirely correct, same as Feudalism and God.

We know enough about neurology in 2021 to understand how neurology is driven and built, by emotions. Emotions are fundamentally resting upon topology, in a sense more fundamental than Category Theory itself (wild hunch on my part!)

A basic failure of old fashion thinking has been to claim that emotion should not influence logic, and, thus, does not influence logic in systems of thought which are advanced enough. That is true in a restricted sense in engineering, technology and some scientific theories… even then the question of why this particular fields have been elaborated and why they are used, arises, unavoidably

Pure logic is an illusion. Axiomatics means choice, thus heresy [1]. 

No saddles for Euclid. So not only did Euclid not ride horses, I presume, but he ignored the computation of the size of the Earth made contemporaneously by Phytas of Marseilles (and generally attributed to Erastothenes, who was born 70 years later, from anti-French racism)

Patrice Ayme

***

P/S: I used “Axiomatics” with an s, the plural, in analogy with “Mathematics”. Thus it is a mild neologism.. But if there is such a thing as “mathematics”, there is certainly such a thing as “axiomatics”, the former being deduced from, and varying according to, the latter…

***

[1] Latin hæresis, “school of thought, philosophical sect.” The Latin word is from Greek hairesis “a taking or choosing for oneself, a choice, a means of taking; a deliberate plan, purpose; philosophical sect, school,” from haireisthai “take, seize,” middle voice of hairein “to choose,”

Mania Form Mafia

As Nietzsche said, folly is rare in the individual, but the rule in the collective. Why it is so is very instructive. I have  explained this: mania cement tribes together, and collective crime unifies best. That doesn’t mean the collective is always wrong. All learning is cultural, thus from a mass of people, thus massive. When an element of culture is erroneous enough, it will bring nefarious consequences… which unite those who believe and participate in that mania. Indeed nothing unites better than common criminality.

It is a fundamental chimp instinct. Then an entire group of chimps get together to go on the warpath, hunt, hurt or, and, kill other chimps, as a matter of territory, hence ecology.

Examples of commonly practiced mania are scapegoatism, another the religion of Abraham, religions with human sacrifices, all sorts of racisms and tribalisms, etc. The crime is not accidental, but unifying. Crimes against truth and common sense are most… common as they present the further advantage of reducing brain work..

Follies are not necessarily useless, far from it. Paradoxically, folly helps reason, by exploring all possibilities, and instills strife, thus it is adaptive to the species which rules the world. Folly suggests and cleanses, by creating the very excesses which identify all the possibilities and diminish the human ecological load. In particular insanity expands the logics to the max. (Yes, this is Erasmus stood on his head…)

The advantage of mass delusions is partly why insanity is rare in the individual but the rule in cultural sets (epochs, nations, religions, etc. Another reason, besides the extremely sophisticated one evoked above is the fact that criminal follies bind tribes best… And plutocracies can exploit these and unite the people that way. See:  “Delusions That Bind”

Belinda Smith

Patrice Ayme

 -I like it, except if you could maybe rephrase the part about the religion of Abraham (singling out Judaism would be anti-Semitic.) For example: most atheists single out no belief. There are also three separate religious groups that come from the Family of Abraham.

Answer to Belinda Smith:

Judeo-Xto-Islamism is just the “religion of Abraham”. Calling them “monotheism” is abusive to other religions which also believed in a supreme being… The religionS of Abraham all emanate from Judaism. It is not anti-Semitic to observe this, because it’s a fact. which can be verified by reading the Bible or the Qur’an (something I do all the time, for fun). As happens with sects, they tend to hate each other. Sunni religious texts (Hadith) enjoin that all jews have to be killed before the Final Judgment can happen. This is not being anti-Jewish or being anti-Sunni to notice this. It is just describing faithfully some related ideologies.

Wisdom cannot listen to the complaints of idiots.

Many view Jesus as a “Rabi”… and Jesus was certainly a Jew… That he was a Jew prevented Christians to exterminate Jews (although they came close many times)… Christians, or more exactly Catholics, exterminated everybody else (99.99% of Samaritans, 100% Cathars, etc.).

Muhammad took refuge in Yattrib, a Jewish city, but later eradicated a Jewish tribe there. And elements of Islam are very clear that Jews are a serious problem with a lethal solution (once again, not an interpretation singling out a religion groundlessly, it’s literally there, in writing).

The Republican Romans outlawed all religions which practiced human sacrifices (so the Celtic religion was 100% eradicated, and the Carthaginian religion went underground). I will review the essay for possible anti-Semitic misrepresentation, though. I am agnostic (I do not pretend to be god by claiming there is no god).

Graduating from the human sacrifice mood as a unifier advanced civilization. One point I make is that the religions celebrating Abraham as founder (Islam, Xtianism, Judaism) celebrate the willingness to commit infanticide to please the boss as a community building criminal mood… In a way that was just not so blatant as to fall under Roman interdiction. So, basically, Abrahamism fosters the mood to do anything to please the boss.

https://patriceayme.wordpress.com/2009/06/22/some-violence-in-holy-quran/

Listening to Christian preachers of US Protestantism (“Reform”) one basically listen, under the para ble of the Jewish people seizing land “given by God”, to the praising, as a religion, of the seizure of land, making war to, and killing the original inhabitants (who were, I think, Semites, nota bene…)

Collective madness is a complicated subject, with pros and cons. One may want to keep that in mind as Internet censorship is ever more practiced all over (not just Xi’s dictatorship).

Patrice Ayme

Better Rationality Forces “Irrational” Jumps

“It’s reasonable to expect people to NOT behave reasonably. Especially innovators.” Discuss.

This essay below is a set of trivial remarks, however, they apparently need to be made. It is standard to oppose and contrast “reason” and “irrationality“. The idea, the hidden axiom in this, classically taken for granted since the so-called Enlightenment, is that the two domains, reason and unreason, are mutually exclusive. However, that’s not correct: reason and unreason are entangled. One doesn’t go without the other. Indeed, the elaboration of any new logic requires to break or supercede the preceding logic. Thus the act of creation of significantly new logic can always be called irrational… from the preceding logic’s reference frame.

Any logic L1 is derived from a finite number of axioms. Any discovery, itself factual, emotional or… logical, if not a consequence of these preceding axioms will require another logic L2. Going from L1 to L2 is only logical in a Meta Logic, LM. In any case L2 and LM are NOT rational in L1. That means irrationality is what feeds rationality!

Thus one sees that one needs irrationality to perfect new, better, improved rationality. Hence, one can see that any better system of thought is going to be attacked as irrational… Because, in a sense, the old sense, it always is so. One may even say that any major advance in understanding, a change of paradigm, will be characterized as not just appearing, but being “irrational“. [1]

Suppose a logic L1 is found to have just ONE flawed axiom. Then one needs to change the axiomatics of L1, and a completely new logic is born, L2. It may, or may not, contain the logic L1. The nature of the change is decided by the application of still another logic, a metalogic, LM.

The jump from L1 to another logic L2 should be called “well ordered” when L2 contains L1. For example turning Newtonian style gravitation into a field theory (a turn initiated I think by Laplace, and fully exploited by Einstein and company), created a theory with a finite interaction speed which contains Newton’s theory. (Well ordering corresponds to L1 being a subcategory of L2…)

By the way, Sub Quantic Physical Reality, my own SQPR, does exactly this finite interaction speed trick to Quantum Theory (L1), and Dark Matter pops out… To use set theory symbolic: QM C SQPR, so the logical switch is well-ordered… (On the other hand, MOND theories, which have been proposed to dispel DM, are not well ordered with Newton gravitation…)

The  shock from L1 to L2 can be brutal, especially when L1 contains blatant lies, or, even worse, excruciating stupidities. An example is the creation of the world according to Jesus and company: creating all the world 6,000 years ago was immensely stupid. Indeed, it used to be well known that animals evolved, since domestication exists (the last 10,000 years in the most advanced parts). A mix of human and natural selection was practiced in ancient Greece, 25 centuries ago to breed world famous superior cattle…. Switching from “God” having created all the species 6,000 years ago to what people have practiced for 10,000 years required more than recognizing one’s naivety. Those who believed in the 6,000 year old magic (that included Newton, it is said…) found very hard to switch to the obvious, as they had to admit they were idiots, to have believed in a stupid theory… Or as it compromised the Christian church and its associated fascist imperialism. For example, Napoleon threatened Lamarck in various ways, as Napoleon was keen to show his attachment to the Christian view of the world.

Jean-Baptiste de Lamarck handing the book ‘Zoological Philosophy’ to Emperor Napoleon Bonaparte, 1920 (pastel on paper) by Ezuchevsky, Mikhail Dmitrievich (1880-1928); State Darwin Museum, Moscow.  The French naturalist research professor at the prestigious Museum d’Histoire Naturelle, Paris, Lamarck (1744-1829) published ‘Philosophie zoologique’ in 1809. In it, Lamarck outlined two new mechanisms to fosters evolution (which he had demonstrated on mollusk fossils). One corresponds to present day epigenetics… The other is probably true, as a consequence of Quantum Theory (to be demonstrated in the future)… Lamarck, having demonstrated evolution scientifically, as a process over millions of years, was hated by the Christian Church… and thus Napoleon. Lamarck is wearing the costume of a member of the Institut de France. Lamarck had become a member of the French Academy of Sciences in 1779, 30 years exactly before his confrontation with Napoleon. Anglo-Saxon ideology dislikes Lamarck, as he was outlawed in English universities. Lyell and Darwin were instructed in his science at Edinburgh, Scotland, more than a decade after the scene above.

Another example: I believe there is only a finite number of numbers, and probably most people who know mathematics will accuse me to be crass ignorant as they would (erroneously) believe in the simple, elementary school 3,000 year old demonstration of infinity… which I can demonstrate is false, and then, rendered perfectly mad by the fact they didn’t see something obvious would scream I deny calculus too (no, calculus works in computers, and computers use only a finite number of operations).

We are in times, and in a situation, where an unimaginable catastrophe is upon us. We need new ideas, new emotions, completely new logic. We will be called names and threatened as we propose them. My daughter’s elementary school proposed to install a gigantic, very expensive ($200,000) artificial grass cum artificial toxic soil, field containing at least three different products know by the State of California to cause cancer (that’s “California Proposition 65“): urethane, (artificial) silica sand, polyurethane… As my spouse pointed this out to the school administration, our daughter, the best student, overall, at her grade level (nota bene), was threatened with immediate expulsion, if we talk to ANYONE about this, through “ANY medium”, and “similar activities”. Somebody is getting something out of this, and we don’t know what it is… But they are really angry about it.

That, while the Secretary of the United Nations just declared war on plastics… Sure enough, the USA was one of a few nations, in contrast to 187, which refused to sign an amendment to the Basel Convention on pollution addressing plastic [2]. Since I don’t like increased plastic usage, either, it makes sense that my daughter be threatened with expulsion.

So you see, any change, even something as simple as any proposition to keep natural grass, is hard, and can involve unforeseen dangers, and punishment with outrageous injustice… and threats against children are an old stand-by: how can the little ones defend themselves?

Changes of logics are hard, so everybody prefer to defend their own turf. All too many ecologists hate nuclear: that’s so simple. Never mind that nuclear gives us life, in more than one way… Right now, 93% of the energy created in 2019 (“primary energy production”) is from MAKING CO2. To diminish this only a massive effort on the three forms of nuclear energy (fission, thorium, fusion) and hydrogen (for storage of renewable energy) can work. Solar is not enough.

What human beings do best, is changing logics. This is also most expensive, and thus what they hate, & resist most fiercely: their advantage, or their survival, is at stake. It’s all about turf. Logical turf in the situations we consider. You see, there is only a limited amount of turf available, mental or physical. To avoid having too much people on a single piece of turf, the species has evolved to engage into violence against each other. That makes the stakes of human logical evolution quite high: those who don’t think correctly are threatened with extinction. In real life. Just as species are extinguished if they are not fit enough, in real life.

All this is very practical: it explains a lot of the hatred around. it is also crucial for advancing science at the highest level. Newton famously debated these questions extensively, modifying the editions of his Principia accordingly, and hiding carefully the existence of a meta logic which had driven him, as he admitted in previous editions! Du Chatelet, writing a bit later was much better on all this, but she was a woman… So only Newton left his mark, all too long…

All this to say that, to think anew is to suffer… if not between the ears, certainly, from others…

Patrice Ayme

***

***

[1] Kuhn may, or may not, have said this, in his famous book on the “Structure of Scientific Revolutions“.

***

[2] The Basel Convention on the Control of Transboundary Movements of Hazardous Waste and their Disposal, which is backed by 187 countries excluding the U.S…

What Is A Logic? Just A Piece Of Mind

I would propose that a logic is anything which can be modelled with a piece and parcel of brain.

I will show, surprisingly enough, that this is a further step in Cartesian Logic.

At first sight, it may look as if I were answering a riddle, by further mysteries. Indeed, but with mysteries which can be subjected to experimental inquiry (now or tomorrow).

What is a brain? A type of Quantum Computer! And what is Computing, and the Quantum? Well, works in progress. There is something called Quantum Logic, but it does not necessarily defines the world, as exactly what Quantum Physics is, is still obscure.

In practice? Logic is what works, a set of rules to go from a set A of statements to a set B of statements.

In this perspective, Medieval logic did not decline. Instead it transmutated into mathematics.

The teaching of Logic or Dialetics from a collection of scientific, philosophical and poetic writings, French, 13th century; Bibliotheque Sainte-Genevieve, Paris, France. The 13th century was a time of extreme intellectual activity in Europe, superior to anything else in the world, centered 800 miles around Paris. In particular the heliocentric system was proposed by Buridan, after he overthrew Aristotelian Physics, by inventing and discovering inertia.

An article in Aeon, “The Rise And Fall And Rise Of Logic”,

https://aeon.co/essays/the-rise-and-fall-and-rise-of-logic

Reflects on the importance on the history of the notion of logic:

“Reflecting on the history of logic forces us to reflect on what it means to be a reasonable cognitive agent, to think properly. Is it to engage in discussions with others? Is it to think for ourselves? Is it to perform calculations?

In the Critique of Pure Reason (1781), Immanuel Kant stated that no progress in logic had been made since Aristotle. He therefore concludes that the logic of his time had reached the point of completion. There was no more work to be done. Two hundred years later, after the astonishing developments in the 19th and 20th centuries, with the mathematisation of logic at the hands of thinkers such as George Boole, Gottlob Frege, Bertrand Russell, Alfred Tarski and Kurt Gödel, it’s clear that Kant was dead wrong. But he was also wrong in thinking that there had been no progress since Aristotle up to his time. According to A History of Formal Logic (1961) by the distinguished J M Bocheński, the golden periods for logic were the ancient Greek period, the medieval scholastic period, and the mathematical period of the 19th and 20th centuries. (Throughout this piece, the focus is on the logical traditions that emerged against the background of ancient Greek logic. So Indian and Chinese logic are not included, but medieval Arabic logic is.)”

The old racist Prussian, Kant, a fascist, enslaving cog in the imperial machine turned false philosopher was unsurprisingly incorrect.

The author of the referenced article, Catarina Dutilh Novaes, is professor of philosophy and the Rosalind Franklin fellow in the Department of Theoretical Philosophy at the University of Groningen in the Netherlands. Her work focuses on the philosophy of logic and mathematics, and she is broadly interested in philosophy of mind and science. Her latest book is The Cambridge Companion to Medieval Logic (2016).

She attributes the decline of logic, in the post-medieval period known as the Renaissance and the Enlightenment, to the rise of printed books, self-study and the independent thinker. She rolls out Descartes, and his break from formal logic:

Catarina writes: “Another reason logic gradually lost its prominence in the modern period was the abandonment of predominantly dialectical modes of intellectual enquiry. A passage by René Descartes – yes, the fellow who built a whole philosophical system while sitting on his own by the fireplace in a dressing gown – represents this shift in a particularly poignant way.”

Speaking of how the education of a young pupil should proceed, in Principles of Philosophy (1644) René Descartes writes:

After that, he should study logic. I do not mean the logic of the Schools, for this is strictly speaking nothing but a dialectic which teaches ways of expounding to others what one already knows or even of holding forth without judgment about things one does not know. Such logic corrupts good sense rather than increasing it. I mean instead the kind of logic which teaches us to direct our reason with a view to discovering the truths of which we are ignorant.

Catarina adds: “Descartes hits the nail on the head when he claims that the logic of the Schools (scholastic logic) is not really a logic of discovery. Its chief purpose is justification and exposition.”

Instead, Descartes claims and I claim that a new sort of logic arose: Medieval Logic transmuted itself into mathematics (Descartes does not say this, but he means it). And mathematics is not really logical in the strictest sense. As it has too many rules to be strictly logical.

Buridan, a great logician who studied well the Liar Paradox (which gave the Incompleteness Theorems) had students such as (bishop) Oresme, who demonstrated what, it turned out, were the first practical theorems in calculus (more than 2 centuries before the formal invention of calculus by Fermat, and Fermat’s discovery of the Fundamental Theorem of Calculus, that integration and differentiation are inverse to each other).

For example, under the influence of Buridan and then Oresme, graphs and later equations themselves were invented. So logic became mathematics. That was blatant by the time Descartes invented Algebraic Geometry. Algebraic Geometry gave ways to deduce, to go from a set A to a set B, using a completely new method never seen before.

In turn, by the Nineteenth Century, mathematical methods contributed to old questions in Logic (the most striking being the use of Cantor Diagonalization to show incompleteness, thanks to the Liar Paradox, self-referential method.

In this spirit, not only Set Theory, naive or not, but Category Theory can be viewed as types of logic. So is, of course, computer science. Logic is whatever enables to deduce. Thus even poetry is a form of logic.

Logic is everywhere there is mental activity, and it is never complete.

If logic is just pieces of brain, then what? Well, some progress in pure logic can be made, just paying attention to how the brain works. The brain works sequentially, temporally, with local linear logics (axonal and dendritic systems). The brain tends to be deprived of contradictions (but not always, and nothing infuriates people more, than to be exposed to their own contradictions and gaps in… logic). Also all these pieces of brain, these logics, are not just temporally ordered, but finite.

As we try to use logic to look forward, as a bunch of monkeys messing up our space rock, it is important to realize that what logic is, has not been properly defined, let alone circumscribed. Indeed, if, surprise, surprise, logic has not been properly defined, let alone circumscribed, much more is logically possible than people suspect!

Patrice Ayme’

 

Mentality Trumps Logic

Mental States Trump, Prime and Build (Local Linear) Logic

How do people think? When thinking about thinking, intellectuals tend to go back to Plato describing the mythical Socrates ponderously going from a) to c) because a) implied b) and b) implied c). Well, this is NOT how the brain works. The brain has basically two systems: Local Linear Logic, and Topological Logic (TL = emotion, so we will call it ES, the Emotional System). LLL and ES are entangled. For example, ES, the Emotion System, shuts off, and opens, various sub-systems in the brain. Moreover the ES directs consciousness into these subsystems. Each of these systems comes with its own logic. So there is no such a thing as “logic” per se. 

Actually modern axiomatics in logic considers that any Logic L comes with its own Universe U (in which it sits, so to speak). Varying U varies L. Thus a Logic L in the brain, sitting in subsystem S1 will be different from one sitting in subsystem S2, because they constitute different universes U. (An aspect of that was long known, as thinkers argued that various drugs, from alcohol to THC enabled them to reach various stages of consciousness…)

Thus what Plato talked about is basically irrelevant to foster wisdom. What is relevant is mental subsystems selection, how, and why. And even subsystem management. Instead, Plato explores logic, LLL. And recent events have been enlightening: LLL is mostly secondary for directing people’s behavior. 

I Think, Therefore I Sting. At Least, Sometimes, I Feel That Way.

By “Trump Madness” I do not mean Trump is mad, far from it: after all, he is the next president, and already causing more change than Obama did in 8 years (see Europe dumping “austerity” within 30 hours of Trump’s election). Clearly, there was a very smart method to Trump’s madness, and it was highly successful for him, as he obtained the loftiest job in the world (at least as far as conventional wisdom has it; in truth the loftiest job is mine, but never mind…). Thus “Trump madness” was anything except madness, on the part of Trump… Or his supporters (who also got what they wanted).

The real madness has been the flow of insults and indiscriminate violence on the part of “Clinton” supporters. Innocent thinkers were called “unscholarly, uncouth, anti-semitic, racist, xenophobic, judged to have Obsessive Compulsive Disorder,  and compulsive liars”. This was just a sampler of the most polite insults directed at me… by “friends”… and I am NOT a Trump supporter. Just thought to be so, because I rolled out all sorts of graphs depicting demoncracy (from inequality, to incarceration, rate, to life expectancy, to government investment, etc.).

Never mind that this was all for positions I held sometimes for decades, they are all extremely progressive, and I am just culprit of having Trump embracing them.

Insults directed at Trump were often obviously more insane than grievous. Trump was called “xenophobic” (the evidence is, the exact opposite, that is, Trump is an extreme xenoPHILE). Trump was called “anti-semitic” (his beloved and trusted son-in-law is an observant Jew). Trump was called a business failure (he grew his “organization”, now in 60 countries, from 17 million dollar to somewhere around ten billion…)

How come Clinton supporters became so abusive? OK, they were surprised. Not just because people were scared to reveal in the polls that they would vote for Trump, skewing polls (pollster Nate Silver discovered this a week or two before the vote, so he “unskewed” the polls, and revealed the chances of Trump were significant; I knew for months, just talking to people, that people were hiding their Trump preferences).

Clinton supporters did not turn abusive and insulting just because what they worry about turns out not to be what most of the country worries about. But, mostly, they hated, because it turned out that they had become strangers to themselves, and the world. Part of them rose in fury, and took over their persona, because they wanted to lash out, so great was the pain that uncomprehension caused..

The Clinton supporters had no idea how neurohormonally entangled with (their idea of) their candidate. Precisely because they were deliberately ignored the (left, leftist, liberal, progressive) case I have made for more than eight years (with all those graphs), they had turned into fanatics, Jihadists, because they had rejected (the unsavory) reality.

The mental order in the brains of these self-described progressives, supposed to address politics, had become hopelessly disconnected from reality. For example, in judging Obama, they judged his brown skin, but not the fact Obama was led by the nose by Lawrence Summers, the Harvard-Goldman Sachs surrogate who had dismantled, under Bill Clinton, the Banking Act of 1933 (“G-S”). And this, seven months before Obama reigned. And they ignored hundreds of other indicators which were flashing way more right, and corporate fascism, than any other president before.

Thus the mental subsystems Clinton supporters activated over the years made them not just unreal, but incapable of activating anything else. One of my prefered game these days is to question Clinton-Obama fanatics about Quantitative Easing. I generally draw a blank. The self-perceived) most clever ones tell me it was a good thing. So here you have so-called progressives saying that giving more than ten trillion dollars to the world richest, most corrupt people and institutions was… a good thing.

Guess what, you dummies? It was a good thing only for plutocracy, also known as demoncracy. The only person who could understand what I was talking about, and agreed with me, before meeting me, is Senior VP in a major bank.

People think first with their neurohormones. Tell me their neurohormones most active, and I can tell you where their Local Linear Logic delves. Obsessions leads and localizes reflection.

Is there experimental evidence for the preceding? Yes, there is, from… insects. The theory of consciousness is starting to rise. It involves making flies play videogames, or seeing if, like American students, they can get scared. Flies can be put in a state of “scariness” and wanting to get to a “safe space”.

Insects have a rudimentary ego, though very different from Narcissus or classical literature would have it. Insect ego appears as the ability to act and mentally concentrate on certain environmental cues thus ignoring others. “They don’t pay attention to all sensory input equally,” cognitive scientist Andrew Barron of Australia’s Macquarie University declared.

When you and I are hungry, we don’t just move towards food, as bacteria do. Our hunger creates a particular feeling (an emotion) which, in turn rearrange which subsystems are activated in our brain. Such a state is called a “subjective experience” in traditional philosophy. Do insects have the same? Obviously they do (I can say from anecdotes, and thus as a philosopher; scientists will verify and make sure).

Insects can be led into mental states which do not fit reality. So can humans (humans even do this deliberately, when they play or make jokes). Once in such a state, a particular logic, the universe of which is that precise mental state, flows. That Local Linear Logic is particular, yet it leaves (neural) connections behind. If suddenly precipitated, for real, in a situation calling for that mental state, the LLL is ready to kick in. That’s why humans play, and make jokes.

This election was a joke. So were the mental states most citizens put themselves, or let themselves been put, in the last few decades. Time to wake up.

And time to wake up to the reality that it is moods which create logic, even more than it is logic which creates moods.

Some will rise their hands in surrender, reading this. They will see logic as defeated. But, well, not at all. Quite the opposite. That mentality trumps logic means logic has to go meta, meta on mentality. One can’t just be logical, to defeat enemy logic. Enemy logic, like ours, is grounded in mentality, and emotion. The fight has to be carried there, it’s not just logical, it’s metalogical.

Patrice Ayme’

***

***

And example of emotion underlying logic has been TDS. TRUMP Derangement Syndrome (TDS) Is MENTALLY ENLIGHTENING, so thank you, all of you, clueless pseudo-progressives, for providing us with not just entertainment, but insights on how insects and other animals think. They think, because they sting. Most people with TDS are at a loss to inform us what progress should be made of, because they lose emotional power, contemplating progress. All the emotions they have tend to underlay their dislike of Trump. I personally disliked Trump 30 years ago, and find him rather improved, nowadays… And, on the progress side, I get more emotional than in my dislike of just one individual… 

Happy In the Sky With New Logics: Einstein’s Error II

Einstein assumed reality was localized and definite in one of his famous 1905 papers, and physics never recovered from that ridiculous, out-of-the-blue, wanton, gratuitous error. (The present essay complements the preceding one found in the link). 

At the origin of Quantum Mechanics is Max Planck’s train of thought. Max demonstrated that supposing that electromagnetic energy was EMITTED as packets of energy hf explained the two obvious problems of physics; h is a constant (since then named after Planck), f is the frequency of the light.

Then came, five years later, Einstein. He explained the photoelectric effect’s mysterious features by reciprocating Planck’s picture: light’s energy was RECEIVED as packets of energy hf. Fine.   

However, so doing Einstein claimed that light, LIGHT IN TRANSIT, was made of “LICHT QUANTEN” (quanta of light), which he described as localized. He had absolutely no proof of that. Centuries of observation stood against it. And the photoelectric effect did not necessitate this grainy feature in flight, so did not justify it.  

Thus Einstein introduced the assumption that the ultimate description of nature was that of grains of mass-energy. That was, in a way, nothing new, but the old hypothesis of the Ancient Greeks, the atomic theory. So one could call this the Greco-Einstein hypothesis. The following experiment, conducted in 1921, demonstrated Einstein was wrong. Thus the perpetrator Walther Gerlach, did not get the Nobel, and the Nobel Committee never mentioned the importance of the experiment. Arguably, Gerlach’s experiment was more important than any work of Einstein, thus deserved punishment The Jewish Stern, an assistant of Einstein, got the Nobel alone in 1944, when Sweden was anxious to make friends with the winning “United Nations”: 

Two Points. The Classical Prediction Is A Vertical Smear. It Is Also Einstein’s Prediction. And That Smear Is Incomprehensible In Einstein’s View Of The World.

Yet, Einstein’s advocacy of nature as made of grains was obviously wrong: since the seventeenth century, it was known that there were wave effects ruling matter (diffraction, refraction, Newton’s rings). That was so true, Huyghens proposed light was made of waves. Around 1800 CE Young and Ampere proposed proofs of wave nature (2 slit experiment and Poisson’s dot). The final proof of the wave theory was Maxwell’s completion and synthesis of electromagnetism which showed light was an electromagnetic wave (travelling at always the same speed, c).

Einstein’s hypothesis of light as made of grain is fundamentally incompatible with the wave theory. The wave theory was invented precisely to explain DELOCALIZATION. A grain’s definition is the exact opposite.

There is worse.

Spin was discovered as an experimental fact in the 1920s. Interestingly it had been discovered mathematically by the French Alpine mathematician Elie Cartan before World War One, and stumbled upon by Dirac’s invention of the eponymous equation.  

The simplest case is the spin of an electron. What is it? When an electron is put in a magnetic field M, it deviates either along the direction of M (call it M!) or the opposite direction (-M). This sounds innocuous enough, until one realizes that it is the OBSERVER who selects the direction “M” of M. Also there are two angles of deviation only. (The Gerlach experiment was realized with silver (Ag) atoms, but the deviation was caused by a single electron therein.)

Einstein would have us believe that the electron is a grain. Call it G. Then G would have itself its own spin. A rotating charged particle G generates a magnetic field. Call it m. If Einstein were correct, as the direction of M varies, its interaction between the grain G magnetic field m will vary. But it’s not the case: it is as if m did not count. At all. Does not count, at all, whatsoever. It’s all about M, the direction of M.

So Einstein was wrong: there is no grain G with an independent existence, an independent magnetic filed m.

Bohr was right: Einstein was, obviously, wrong. That does not mean that Bohr and his followers, who proclaimed the “Copenhagen Interpretation” were right on other issues. Just like Einstein hypothesized something he did not need, so did the Copenhagists.

Backtrack above: M is determined by the observer, I said (so bleated the Copenhagen herd). However, although M can changed by an observer, clearly an observer is NOT necessary to create a magnetic field M and its direction.

Overlooking that blatant fact, that not all magnetic fields are created by observers, is the source of Copenhagen confusion.

We saw above that correct philosophical analysis is crucial to physics. Computations are also crucial, but less so: a correct computation giving correct results can be made from false hypotheses (the paradigm here is epicycle theory: false axiomatics, the Sun did not turn around the Earth, yet, roughly correct computations produced what was observed).

Out of Quantum Theory came Quantum ElectroDynamics (QED), and, from there, Quantum Field Theory (QFT).  

QED is one of the most precise scientific theory ever. However, there is much more precise: the mass of the photon is determined to be no more than 10^(-60) kilogram (by looking at whether the electromagnetic field of Jupiter decreases in 1/d^2…).

Nevertheless, QED is also clearly the most erroneous physical theory ever (by an order of 10^60). Indeed, it predicts, or rather uses, the obviously false hypothesis that there is some finite energy at each point of space. Ironically enough, it is Einstein and Stern (see above) who introduced the notion of “zero point energy” (so, when Einstein later could not understand, or refused to understand, Quantum Electrodynamics, it was not because all the weirdest concepts therein were not of his own making…)

The debate on the Foundations of Quantum Physics is strong among experts, all over the map, and permeated with philosophy. Thus don’t listen to those who scoff about whether philosophy is not the master of science: it always has been, it is frantically so, and always will be. It is a question of method: the philosophical method uses anything to construct a logic. The scientific method can be used only when one knows roughly what one is talking about. Otherwise, as in Zeroth Century, or Twentieth Century physics, one can go on imaginary wild goose chases.

From my point of view, Dark Matter itself is a consequence of the True Quantum Physics. This means that experiments could be devised to test it. The belief that some scientific theory is likely incites beholders to make experiments to test it. Absent the belief, there would be no will, hence no financing. Testing for gravitational waves was long viewed as a wild goose chase. However, the Federal government of the USA invested more than one billion dollars in the experimental field of gravitational wave detection, half a century after an early pioneer (who was made fun of). It worked, in the end, splendidly: several Black Hole (-like) events were detected, and their nature was unexpected, bringing new fundamental questions.

Some will say that all this thinking, at the edges of physics and philosophy is irrelevant to their lives, now. Maybe they cannot understand the following. Society can ether put its resources in making the rich richer, more powerful and domineering. Or society can pursue higher pursuits, such as understanding more complex issues. If nothing else, the higher technology involved will bring new technology which nothing else will bring (the Internet was developed by CERN physicists).

Moreover, such results change the nature not just of what we believe reality to be, but also of the logic we have developed to analyze it. Even if interest in all the rest faded away, the newly found diamonds of more sophisticated, revolutionary logics would not fade away.

Patrice Ayme’

 

HUMANITY: A SINGULARITY

HUMANITY: Not Just Singular.

The Human Condition: never so contingent, that we are forever prisoner of it.

Some worry about, others anticipate “the singularity”, when human technology exponentiates for all to see. Many expect that it is coming soon. But “the singularity” has long been around. We have been living through it, ever since human evolved, and they started to think in all-devouring ways, a couple of million years ago. The invention of mass transmissible global culture, hundreds of thousands of years ago, launched us towards the stars.

What’s science for? Aside from keeping our world up in the air? Science is what is known for sure. A (good) mom knows to love for sure. So, alright, there is a science of love. Human beings, as are many animals, all the way down to insects, are naturally equipped not just to know, but to understand what they needed to understand to survive as a species.

Art: Beautiful & Interesting, In Part Because It Reveals Logic Never before Suspected, Or Because It Reminds Us Of Them. When God Is Shows His Consideration For Us, We Are Made Into The Crown Of Creation & The Transmission of Power, Knowledge Are Impressed Upon Us As The Most Important Activities Worthy Of The Gods We Are

Orphaned earwigs, a type of insect, are at a disadvantage and exhibit reduced maternal skills. Beauty and love are everywhere. Transmission of knowledge is what brains do.

Humanity itself is a singularity of mind the evolution of creation  (“life”) has blossomed into. Our technologies (“specialized discourses”) expanded over all of Earth, and expanded what Earth could be for us, as Earth itself became our province. And this physical empire did so because our minds expanded. Earth became an empire of reason (in particular, very hot, crazy reasons). Our minds expanded so much that they not just revealed, but caused, accordingly, new, spectacular problems… which we presently enjoy ever more.

Science is not just a knowledge of facts, but a knowledge of beauty which would not have been otherwise revealed. Science is also the uncovering of logic of previously unsuspected subtlety, for all to see. Thus subjects as esoteric as how exactly supernovae explode can reveal how explanations can go about things.

Beauty itself, is partly a matter of logic: when god touches humanity with its finger in Michelangelo’s famous painting, the beauty depicts a logic, and it is what makes it, in part, beautiful.

On March 21, 2016, NASA and its (crippled, but reconfigured for doing other things) Kepler telescope, revealed the visualization of the explosions of some supernovae.

Knowing about supernovae is not just knowing how the chemistry which made Earth possible was created. It is not just about knowing the size of the universe, and how fast it is changing. It is also knowing about analogies, metaphors, logics and possibilities we never suspected, and also about our naivety, to never have suspected they were.

Our knowledge of facts and logics, and of the beauty and possibilities they entail, are indeed exponentiating (or more). They long have been, it’s our definition.

However, it is now clear that, within a decade or so, most work will be taken over by machines, even work of a creative nature. The human work will have to be the all too human crazy creativity of geniuses, art never thought of before. It is already the case: the economic success of a city such as San Francisco is now mostly from the creation of so-called “apps” which are little computer programs for doing little things one never thought of, or could do, before (or assemblies thereof, such as the notorious “Uber” with its astounding 65 billion dollars market cap).

And we can’t turn back, because it’s what we are: ”Plus Oultre!”. As Charles Quint put it in his native French: Plus Ultra (Motto Of Spain), Plus Meta,

And the biosphere could not handle a U-turn on humanity’s part, weirdly enough. Actually, handling the CO2 crisis will have to be done the old fashion way: through brand new technological means, the exact way in which life already deals with it (after all, plants use CO2 to build themselves with it… although CO2 is notoriously chemically inert, thus nearly useless industrially… so far. But, philosophically speaking, there is no reason why human science can duplicate with CO2 what 4 billion years of molecular biology succeeded to achieve.)

Some may object that the preceding, however alluring, is a sort of sing-song, Patrice perched on a branch, singing to the stars, human, all too human (thus not really marketable).

However, not so. The poorly parented earwigs, these modest insects with big pincers for a tail, are themselves poor parents, because they have undergone genetic changes. They are victims, or, more exactly, creations of epigenetics, what controls genetic itself (and which Lamarck had anticipated). We, the genus Homo, have gone through 100,000 generations of intense selection according to our capability to outsmart our opponents (other, less performing humans, mostly). So we are the mental species, in all sense of the term: crazily creative, and creatively crazy.

This is not just a song, it’s a reality. Our reality. Not just our ethics, but our esthetics are dependent upon the sum of all our evolutionary histories, our genetics and epigenetics, and those progress to ever more understanding, and mastery of the universe, therefrom.

Thus, all speed ahead, we are special, we may as well admit that violating old norms and creating new ones is not just what we do, but what we are.

Patrice Ayme’   

Logic Is Not Everything: It Can Be Anything

A common mistake among many of the simple ones, is that, as long as we keep calm and use logic, we can solve any conflict. It was understandable that one could do such a mistake due to naivety and inexperience, before the Twentieth Century. However, we have now, black on white and well known, demonstrations to the contrary, in formal systems studied by professional logicians. Besides, as The French Republic is demonstrating in Libya again, in collaboration with the USA, war has a logic which squashable critters don’t have.

Yes, I am also thinking of the famous Incompleteness Theorems, but, obviously, not only. There is way worse.

This Means All Important Choice Have to Do With Love, Esthetics, Will, Power, Craziness, The Proverbial Human Factors. Logic Can’t Go Where The Heart Rules. Or Then Go Into METAlogic.

Before I get in incompleteness and further evils, let me recap some of the traditional approach. I thank in passing Massimo P, for calling my attention to this.

The value of logic, February 23, 2016, Massimo

This is going to be short and rather self-explanatory, with no additional commentary on my part necessary at all. Here is the full transcription of Epictetus’ Discourses, II.25, a gem to keep in mind for future use:

“When one of his audience said, ‘Convince me that logic is useful,’ he said, Would you have me demonstrate it?

‘Yes.’

Well, then, must I not use a demonstrative argument? And, when the other agreed, he said, How then shall you know if I impose upon you?

And when the man had no answer, he said, You see how you yourself admit that logic is necessary, if without it you are not even able to learn this much–whether it is necessary or not.”

Actually Epictetus uses “logic”, it seems to me, rather in its original sense, a discourse. Yet Massimo, like the moderns, will tend to use logic as it was meant in, say, 1900, just before Bertrand Russell objected to Frege’s forgetfulness of the “Liar Paradox” in his formal system justifying arithmetic. A further exploitation of the Liar Paradox brought the incompleteness theorems.

Logic is indeed how human beings communicate. Logic enables debate, and debate is the equivalent of sex, among ideas. It generates entirely new species. However post Gottlob Frege and Bertrand Russell, logic has progressed much.

Modern studies in logic show formal logic can be pretty much anything. Formal systems contradicting the most cherished axioms have been found to be consistent. Some have cute names, such as “paradoxical logic”, “fuzzy logic”, “linear logic”. Thus, Logical Pluralism has been discovered. “Classical Logic” (which neither complete nor coherent) is just a particular case. In some logics, a proposition can be neither true, nor false.

Along the line of ones of the greatest logician and mathematicians of the 20th Century, Generalized Tarski Thesis (GTT):
An argument is valid if and only if in every case in which the premises are true, so is the conclusion.
So yes, madness can be logical. “Logic”, per se, is not much of a constraint. It’s only a set of coherent rules to draw a conclusion. The only constraint is to keep on talking.
The Ancient Greeks would have been very surprised.

So if logic is not the end-all, be all, what is?

Knowledge. Knowledge of the details. In other words, knowledge of evil. That is why, when I demonstrate, using knowledge, that Marcus Aurelius, supposedly the big time Stoic philosopher, makes the apology of Intellectual Fascism, I hear the cries of the Beotians, whose pathetic logic have crushed underfoot. What happened? I went outside of their logic. So they insult me. (Should I spurn them, and make them feel that I have nothing to say, or insult them back, by showing them, and others, what idiots they are? Sitting on one’s hand in front of rabid fascism is neither wise, nor safe!)

In other news, French special forces are operating on the ground in Libya, helping, among other things, very precise US strikes. This is a case of using the same logic as the enemy. The Islamists terrorize and kill: a logic which is pretty drastic. It can also be adopted. Let see how it goes, when the country with the greatest, longest military tradition, adopts it too. (France has a long history of drastic war against invading Islamists, since the Battle of Toulouse, in 721 CE)

Speaking of the enemy, the French Internal Revenue Service is forcing Google Inc., the famous monopoly. to pay back taxes. Google has sent the clown it uses as CEO to Paris. Google was transferring profits it made in France through Ireland, and then Bermuda. The bill? 1.6 BILLION Euros. Great Britain has a similar situation and economy, but is asking for only a tenth of that. Such is plutocracy: greater in the UK than in France.

Ah, the French Defense Ministry is not denying media reports that the French army is in combat, on the ground, in Libya. Instead, the French government has announced the start of an inquiry for finding out who compromised National Defense. In other words, it wants it to be known. Or there is much more coming, which it wants to hide. Or then American paranoia is contagious.

In other news, Belgium, historically a part of Gaul, has closed its border with France, as if Belgium were Great Britain, and France, full of Huns (instead of only Afghans). Amusingly, and a testimony of how much old gripes have subsidized, the Franco-German border stays open.

Logic is not all. Facts are much more important, including facts on the ground.

Patrice Ayme’

Causality Explained

WHAT CAUSES CAUSE?

What Is Causality? What is an Explanation?

Pondering the nature of the concept of explanation is the first step in thinking. So you may say that there is nothing more important, nothing more human.

I have a solution. It is simplicity itself. I go for the obvious model:

Mathematics, logic, physics, and the rest of science give a strict definition of what causality, and an explanation is.

How?

Through systems of axioms and theorems.

Some of the sub-systems therein have to do with logic (“Predicate Calculus”). They are found all over science and common sense (although they will not be necessarily present in systems of thought such as, say, poetry, or rhetoric).

WHEN A IMPLIES B, IN A LOGOS, ONE OUGHT TO SAY THAT A “CAUSES” B.

A and B are propositions. They do not have to be very precise.

Precision Is Not Necessarily The Smartest. Semantic Web Necessary.

As it turns out, except in Classical Computer Science as it exists today (Classical CS by opposition to Quantum CS, a subject developing in the last 20 years), propositions are never precise (so a degree of poetry is everywhere, even in mathematics!) Propositions, in practice, depend upon a semantic web.

A could be: “Plate Tectonic” and B could be “Continental Drift”. That A causes B is one of axioms of present day geophysics.

Thus I define causality as logical implication.

To use David Hume’s example: flame F brings heat H, always, and so is supposed to cause it: F implies H. Hume deduced causality from observation of the link (if…then).

More detailed modern physics shows that the heat of flame F is agitation that can be transmitted (both a theorem about, and a definition of, heat). Now we have a full, detailed logos about F and what H means, and how F implies H, down to electronic orbitals.

Mathematicians are used to make elaborate demonstrations, and then, to their horror, discover somewhere something that cannot be causally justified. Then they have to reconsider from scratch.

Mathematics is all about causality.

“Causes” in mathematics are also called axioms. In practice, well known theorems are used as axioms to implement further mathematical causality. A mathematician using a theorem from a distant field may not be aware of all the subtleties that allow to prove it: he would use distant theorems he does no know the proof of, as axioms. Some mathematician’s, or logician’s axiom is another’s theorem.

(Hence some hostility between mathematicians and logicians, as much of what the former use the latter proved, but the former have no idea how!)

Causality, by the way, reflects the axonal geometry of the brain.

The full logic of the brain is much more complicated than mathematics, let alone Classical Computer Science, have it. Indeed, brain logic involves much more than axons, such as dendrites, neurotransmitters, glial cells, etc. And of these, only axonal geometry is simple enough to be approximated by classical logic… In first order.

Mathematics is causation. And the ultimate explanation. Mathematics makes causation as limpid we can have it.

This theory met with the approval of Philip Thrift (March 27, 2015): “I agree exactly with the words Patrice Ayme wrote — but with “mathematics”→”programming”, “mathematical”→”programmatical”, etc.”

I pointed out later to Philip that Classical Programming was insufficient to embrace full human (and quantum!) logic. He agreed.

However the preceding somehow made Massimo P , a professional philosopher, uneasy. He quoted me:

“Patrice: “To claim that mathematics is not causal is beyond belief. Mathematics is all about causality.”

Massimo: It most obviously isn’t. What’s causal about Fermat’s Last Theorem? Causality implies physicality, and most of pure math has absolutely nothing whatsoever to do with physicality.

Patrice: “Causes” in mathematics are also called axioms.”

Massimo: “You either don’t understand what causality means or what axioms are. Or both.”

Well, once he had released his emotional steam, Massimo, a self-declared specialist of “physicality” [sic] did not offer one iota of logic in support of his wished-for demolition of my… logic. I must admit my simple thesis is not (yet) in textbooks…

Insults are fundamentally poetic, illogical, or pre-logical. Massimo is saying that been totally confused about causality and explanations is a sacred cow of a whole class of philosophers (to whom he had decided he belongs). Being confused about causality started way back.

“All philosophers, “said Bertrand Russell,” imagine that causation is one of the fundamental axioms of science, yet oddly enough, in advanced sciences, the word ’cause’ never occurs … The law of causality, I believe, is a relic of bygone age, surviving, like the monarchy, only because it is erroneously supposed to do no harm …”

Russell was as wrong as wrong could be (not about the monarchy, but about “causation”). He wrote the preceding in 1913, when Relativity was well implanted, and he, like many others, was no doubt unnerved by it.

Poincare’ noticed, while founding officially “Relativity” in 1904, that apparent succession of events was not absolute (but depended upon relative motions).

Indeed.

But, temporal succession is only an indication of possible causality. In truth causality exists, if, and only if, a logical system establishes it (moreover, said logic has to be “true”; that, assigning a truth value, is, by itself is a separate question that great logicians have studied without clear conclusions).

When an explanation can be fully mathematized, it is finished. Far from being “abstract”, it has become trivial, or so suppose those with minds for whom mathematics is obvious.

Mathematics is just like 2 + 2 = 4, written very large.

Fermat’s Last Theorem is not different in nature, from 2 + 2 = 4… (But for something very subtle: semantic drift, and a forest of theorems used as axioms to go from side of Fermat’s theorem to the other.)

To brandish mathematics as unfathomable “abstract” sorcery, as was done in Scientia Salon, is a strange, but not new, streak.

There in “Abstract Explanations In Science” Massimo and another employed philosopher pondered “whether, and in what sense, mathematical explanations are different from causal / empirical ones.”

My answer is that mathematical, and, more generally logical, explanations are the model of all explanations. We speak (logos) and thus we communicate our thoughts. Even to ourselves.

The difference between mathematics and logic? Mathematics is more poetical. For example, Category Theory is not anchored in logic, nor anywhere else. It is hanging out there, beautiful and useful, a castle in the sky, just like all and any poem.

Such ought to be the set-up on the nature of what causality could be, to figure out what causality is in the physical world. Considering that Quantum Entanglement is all over nature, this is not going to be easy (and it may contain a hidden clock).

Patrice Ayme’